4.1 Introduction
The estimation of future values of a time-dependent function, based on current and past values of a data sequence representing the function, is known as extrapolation. The estimation of function values between data points is known as interpolation. Both digital extrapolation and interpolation can play an important role in real-time digital simulation of dynamic systems. For example, digital extrapolation can be used to predict future values of a time-dependent function. This can be useful in compensating for delays in signals that are interfaced to the computer. Digital interpolation can be used in the simulation of a pure time delay, often called a transport delay.
One of the most important applications of digital extrapolation and/or interpolation occurs in the generation of a fast data sequence from a slow data sequence. This is necessary in the implementation of multi-rate integration, where a fast dynamic subsystem is integrated with a frame rate that is an integer multiple N of the frame rate used to integrate the slow subsystem. From the data sequence output of the slow subsystem it is necessary to derive a data sequence with N times the sample rate in order to provide the input to the fast subsystem. The use of multi-rate integration within a digital simulation can often be used to improve the accuracy of a real-time digital simulation, or to speed up a non real-time simulation in order to make it more economical to run. This is especially true in the case of many stiff systems, where the ratio of the largest to smallest eigenvalue magnitudes in a quasi-linear representation can be many orders of magnitude.
In this chapter we will develop a number of digital extrapolation and interpolation algorithms and analyze their accuracy in both the time domain and frequency domain. Because the data sequences representing the digital signals are assumed to have a fixed sample period, the method of Z transforms can be used for the frequency-domain analysis, which consists of determining formulas for the gain and phase errors associated with the algorithms. These gain and phase errors provide a basis for selecting the most appropriate algorithm for a given application. The specific case of extrapolation or interpolation to generate a fast data sequence from a slow data sequence is analyzed using a discrete Fourier series to represent the fast data sequence. When the slow data sequence is a sinusoid, this analysis provides formulas for the fundamental and harmonic components present in the fast data sequence. These formulas can in turn be used to estimate the dynamic errors present in the fast data sequence.
4.2 Linear Extrapolation Based on rn, and rn-1
As a first example, we consider digital extrapolation based on the current value, rn, and the immediate past value, rn-1, of a digital data sequence. Let h represent the time between samples. Then we can approximate the time function, r(t), represented by these two data points using the zeroth and first-order terms in a Taylor series expansion about t = nh. Thus we let the approximation 
be given by
(4.1)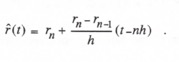 
Here 
is the numerical approximation to 
, as obtained from a backward difference. From Eq. (4.1) we see that 
and 
, so that the approximation function 
passes through the data points 
and 
Next assume that we wish to extrapolate ahead in time by ah seconds, where a represents a dimensionless extrapolation interval. From Eq. (4.1) the extrapolated time function 
, which from now on we will designate as 
, is given by
(4.2) 
For a = 1 the prediction interval ah = h, and 
, the extrapolated value of 
based on 
and 
. Note that for -1 <a<0, Eq. (4.2) represents interpolation between 
and 
The time domain error associated with 
in Eq. (4.2) can be predicted analytically by the following Taylor series:
(4.3) 
For extrapolation based on 
and 
we replace 
with a formula based on 
and 
. This in turn is obtained from a Taylor series formula for 
. Thus
from which
(4.4) 
Substituting Eq. (4.4) into Eq. (4.3), we obtain
(4.5) 
The first two terms on the right side of Eq. (4.5) represent 
, the estimate for 
based on 
and 
, as given in Eq. (4.2). With 
replaced by 
, Eq. (4.5) can be rewritten as
(4.6) 
where 
is the error in the extrapolation formula and is proportional to h2. The error is also proportional to the second time derivative of r.
We now take the Z transform of the difference equation represented by (4.2) in order to obtain the formula for the extrapolator transfer function for sinusoidal inputs. Thus
where 
is the Z transform of the data sequence represented by 
. The extrapolator Z transform, 
, is given by
(4.7)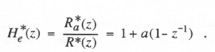 
The extrapolator transfer function for a sinusoidal data input becomes
(4.8) 
An ideal extrapolator with a prediction interval ah has the transfer function 
. For sinusoidal inputs the ideal extrapolator transfer function is given by
(4.9) 
From Eqs. (4.8) and (4.9) we obtain the following formula for the fractional error in the digital extrapolator transfer function:
(4.10)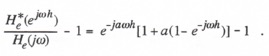 
When the exponential functions are expanded in power series, the following formula is obtained for 
:
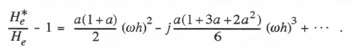
As noted previously in Eqs. (1.53) and (1.54), the real and imaginary parts of 
are equal, respectively, to the fractional gain error and the phase error of the extrapolator transfer function. Thus
(4.11)
Although the formulas in Eq. (4.11) are approximations based on the dimensionless frequency 
being small compared with unity, they are reasonably accurate up to 
for 
. Of course, Eq. (4.10) is exact and can be used to calculate 
and 
for any specific 
and a. From the asymptotic formulas in Eq. (4.11) we note that the extrapolator gain error is proportional to 
and the phase error is proportional to 
. Thus the predominant error will in general be the gain error for extrapolation based on 
, and 
.
4.3 Linear extrapolation based on 
and 
Another method for linear extrapolation is based on using 
and 
, instead of 
and 
. This is possible when both 
and 
are state variables, since under these conditions 
is available at the start of the nth integration frame. In this case the extrapolation formula becomes
(4.12) 
From Eq. (4.12) it is clear that 
. If we let 
, the prediction interval, then from Eq. (4.12) we obtain the following formula for the extrapolated data point 
:
(4.13) 
Taking the Z transform of Eq. (4.13), we have
(4.14) 
For a sinusoidal data sequence with 
, it follows that 
and Eq. (4.14) becomes
(4.15) 
Thus the digital extrapolator transfer function for sinusoidal inputs is given by
(4.16)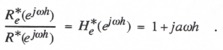 
Dividing 
in Eq. (4.16) by the ideal extrapolator transfer function 
in Eq. (4.9), we obtain the following formula for the fractional error in extrapolator transfer function:
(4.17) 
Expanding the exponential functions in a power series, we obtain the formula
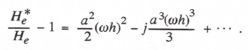
It follows that the asymptotic formulas for the fractional error in gain and the phase error are given by
(4.18)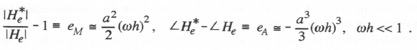 
From Eq. (4.18) we see that here again the extrapolator gain error predominates and is proportional to 
, whereas the phase error is proportional to 
. Comparison of Eq. (4.13) with the exact power series formula for 
in Eq. (4.3) shows that the extrapolator time-domain error, 
, is given by
(4.19) 
As in the case of extrapolation based on 
and 
, the error here for extrapolation based on 
and 
is proportional to 
and also the second time derivative of r. For a sinusoidal data sequence we note that 
. In this case the extrapolator error in Eq. (4.19), when normalized through division by r, becomes 
. This in turn is just the fractional error in transfer function gain, as given above in Eq. (4.18). Similarly, for a sinusoidal input with extrapolation based on 
and 
, reference to Eqs. (4.6) and (4.11) shows that the normalized extrapolator time-domain error becomes the same as the fractional error in transfer function gain.
In Figure 4.1 the transfer function gain errors, as obtained from the asymptotic formulas in Eqs. (4.11) and (4.18) and normalized through division by 
, are plotted versus the dimensionless extrapolation interval a for extrapolation based on 
, 
and 
, 
. For extrapolation based on 
and 
we note that -1 < a< 0 actually represents interpolation between 
and 
rather than extrapolation beyond 
. Figure 4.1 shows that interpolation is in general more accurate than extrapolation when using 
and 
.
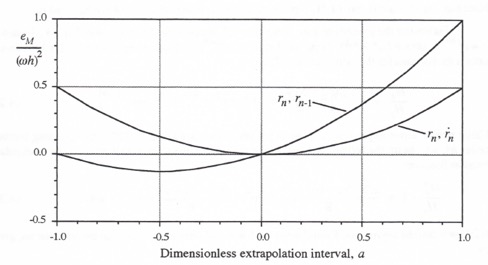
Figure 4.1. Gain error coefficient, 
, versus dimensionless extrapolation interval a for linear extrapolation algorithms.
It should be noted that both 
, 
and 
, 
extrapolation can produce gains appreciably greater than unity when 
exceeds unity. From the exact formula for 
in Eq. (4.8) it can be shown that the gain 
for a given prediction interval a peaks for 
, 
extrapolation at 
. The corresponding peak gain is equal to 1 + a. For extrapolation based on 
, 
it is apparent from Eq. (4.15) that the gain is equal to 
. Ideally, the extrapolator gain should be equal to unity for all frequencies. In general one does not expect significant frequency components above 
in the data sequence corresponding to 
. But any such components can become amplified appreciably when using the first-order extrapolation algorithms considered here.
4.4 Quadratic Extrapolation Based on 
In this and the following two sections we analyze several quadratic extrapolation algorithms. First we consider extrapolation based on the data points 
, 
and 
. When a quadratic function of time is passed through these three points, the following formula results:
(4.20) 
Here the coefficient of (t – nh) is a backward difference approximation to 
, while the coefficient of (t – nh)2 is a backward difference approximation to 
. If we let t = nh+ ah in Eq. (4.20), where ah is the prediction-time interval, we obtain the following formula for the extrapolated data point, 
:
(4.21) 
Note that for -2 < a< 0, Eq. (4.21) represents quadratic interpolation between 
and 
.
Following the procedure used in Section 4.2, we take the Z transform of Eq. (4.21) and let 
to obtain 
. Next we divide by 
, the ideal extrapolator transfer function, to obtain the formula for the ratio 
. Thus
(4.22)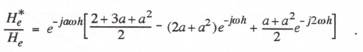 
Using power series expansions for the exponential functions in Eq. (4.22) and retaining terms to order h4, we obtain the following formula for the approximate fractional error in the extrapolator transfer function:
(4.23)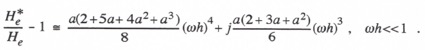 
It follows that the asymptotic formulas for the fractional error in gain and the phase error are given by
(4.24)
Here the phase error predominates for small 
and is proportional to 
, whereas the gain error is proportional to 
.
To obtain the formula for the time-domain error in 
based on 
, 
and 
, we utilize the power series formula of Eq. (4.3) for the exact 
. Additional Taylor series expansions for 
and 
about 
are written, from which we can determine formulas for 
and 
in terms of 
, 
and 
. Substituting these formulas into Eq. (4.3), we obtain the following series representation for 
:
(4.25) 
Comparison with Eq. (4.21) shows that the extrapolator time-domain error, 
, is given by
(4.26) 
For a sinusoidal data sequence we note that 
. In this case the extrapolator error in Eq. (4.26), when normalized through division by r, becomes 
. This in turn is just the transfer function phase error, 
, as given above in Eq. (4.24).
4.5 Quadratic extrapolation based on 
, 
and 
Next we consider extrapolation based on 
, 
and 
. This is possible when both 
and 
are state variables, since under these conditions 
is available at the start of the nth integration frame. The formula is based on a quadratic that passes through 
and 
, and matches the slope 
at t = nh. The resulting equation is given by
(4.27) 
Here the coefficient of 
is the numerical approximation to 
. Substitution of 
into Eq. (4.27) leads to the following formula for the extrapolated data point, 
:
(4.28) 
For -1 < a < 0, Eq. (4.28) represents quadratic interpolation between 
and 
. Following the procedure used in Section 4.2, we take the Z transform of Eq. (4.28) and let 
to obtain 
. Next we divide by 
, the ideal extrapolator transfer function, to obtain the formula for the ratio 
. Thus
(4.29) 
Expanding the exponential functions in power series, we obtain the formula for the fractional error in extrapolator transfer function in series form. From the real and imaginary parts of the series, respectively, we obtain the following asymptotic formulas for the fractional error in gain and the phase error:
(4.30) 
Here the phase error predominates for small 
and is proportional to 
, whereas the gain error is proportional to 
, which is the same result we obtained for the quadratic extrapolator of the previous section.
To obtain the formula for the time-domain error in 
based on 
, 
and 
, we again utilize the power series expansion of Eq. (4.3) for the exact 
. An additional Taylor series expansion for 
about 
is written, from which we can determine a formula for 
in terms of 
, 
and 
to substitute into Eq. (43). From this result we obtain the following formula for the extrapolator time-domain error, 
:
For a sinusoidal data sequence we note that 
. In this case the extrapolator error in Eq. (4.31), when normalized through division by r, becomes 
. This in turn is just the transfer function phase error 
, as given above in Eq. (4.30).
4.6 Quadratic extrapolation based on 
and 
Finally we consider quadratic extrapolation based on 
, 
and 
. This becomes of interest when r is a state variable but 
is not. In this case 
will in general not be available for extrapolation over the nth frame, since it will not yet have been calculated. Here the quadratic time function passes through 
, and 
, and matches the slope 
at 
. The extrapolator formula is given by
(4.32) 
Following the same Z-transform procedure used in the previous two sections, we obtain the following asymptotic formulas for the fractional error in gain and the phase error of the extrapolator transfer function for sinusoidal inputs:
(4.33) 
As in the case of the other two quadratic extrapolation formulas, here the phase error predominates for small 
and is proportional to 
, whereas the gain error is proportional to 
.
As before, the time-domain error in 
based on 
, 
and 
is determined from the power series expansion of Eq. (4.3). Additional Taylor series expansions for 
and 
are written, from which we can determine formulas for 
and 
in terms of 
, 
and 
to substitute into Eq. (4.3). From these results we obtain the following formula for the extrapolator time- domain error, 
:
(4.34) 
Again, for a sinusoidal data sequence, 
, and the extrapolator error in Eq. (4.34), when normalized through division by r, becomes 
. This is just the transfer function phase error 
, as given above in Eq. (4.33).
In Figure 4.2 the transfer function phase errors, as obtained from the asymptotic formulas in Eqs. (4.24), (4.30) and (4.33) and normalized through division by 
, are plotted versus the extrapolation interval a for the three quadratic extrapolation algorithms considered here. Again we note that 0 < a < 1 represents extrapolation and -1 < a < 0 represents interpolation. Clearly, interpolation is much more accurate than extrapolation. It is also evident that the algorithm based on 
, 
and 
produces the most accurate results.
4.7 Cubic extrapolation based on 
and 
Although there are a number of possible cubic extrapolation algorithms, in this section we will consider only one, which is based on a cubic function that passes through the data points 
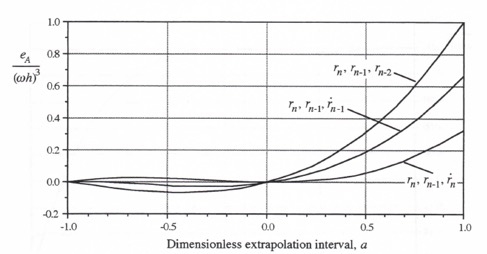
Figure 4.2. Phase error coefficient, 
, versus dimensionless extrapolation interval a for quadratic extrapolation algorithms.
and 
and matches the slopes 
and 
. In this case the formula for the extrapolated data point, 
, is given by
(4.35) 
If 
and 
are state variables in the simulation, then 
and 
are available for the algorithm. Following the same procedure used in Section 4.3 for 
in extrapolation, we can derive the extrapolator transfer function for sinusoidal inputs, 
. After dividing by the ideal extrapolator transfer function, 
, we obtain the following formula for the ratio 
:
(4.36) 
The asymptotic formula for the fractional error in extrapolator transfer function is obtained by subtracting 1 from the right side of Eq. (4.36) and replacing the exponential functions with power series. Retaining terms up to order 
, we obtain the following asymptotic formulas for the fractional error in gain and the phase error from the real and imaginary parts of the series:
(4.37) 
For this cubic extrapolation algorithm the predominant error is the gain error, which is proportional to 
. Figure 4.3 shows a plot of the error coefficient, 
, as given in Eq. (4.37), versus the dimensionless extrapolation interval a. In the case of this third-order algorithm the difference between the interpolation errors (-1 < a< 0) and the extrapolation errors (0 < a< 1) is very substantial. For example, the peak gain-error magnitude for interpolation, which occurs at 
, is
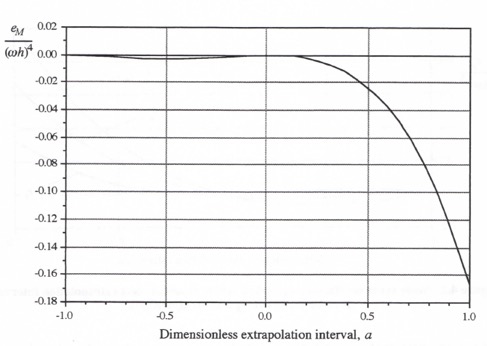
Figure 4.3. Gain error coefficient, 
, versus dimensionless extrapolation interval a for third-order extrapolation based on 
and 
equal to 1/384. By comparison, the peak gain-error magnitude, which occurs at a = 1, is equal to 1/6.
From the appropriate Taylor series expansions the following formula for 
, the time-domain error of the third-order extrapolator, can be derived:
(4.38) 
For a sinusoidal data sequence, 
, and the extrapolator error in Eq. (4.38), when normalized through division by r, becomes 
. This is just the transfer function gain error 
given above in Eq. (4.37).
From the exact formula for 
the transfer function gain, 
, can be determined from Eq. (4.36) for the case where the input frequency 
is not small compared with unity. For a = 1 and 
, the gain increases rapidly with increasing 
. For example, for 
. Since the gain for a < 1 is proportional to a2, it will be considerably less for smaller extrapolation intervals a. In the unlikely event that the data sequence corresponding to 
has significant frequency components for which 
, although 
can never exceed 
(see Section 5.10), the third-order extrapolation algorithm considered here will amplify such high-frequency components appreciably.
4.8 Summary Tables of Extrapolator Formulas and Transfer Function Errors
The extrapolator formulas developed in Sections 4.2 through 4.7 are summarized in Table 4.1. Table 4.2 presents the asymptotic formulas for the gain and phase errors of the corresponding extrapolator transfer functions.
Table 4.1
Summary of Extrapolator Formulas
Table 4.2
Summary of Extrapolator Transfer Function Gain and Phase Errors
4.9 Generation of Multi-rate Data Sequences
In this section we consider the generation of fast data sequences from slow data sequences, i.e., the generation of multi-rate data sequences. In Section 4.1 we have already noted that this is required in the implementation of multi-rate integration, where a fast dynamic subsystem is simulated with an integration frame rate that is an integer multiple N times the integration frame rate used to simulate the slow subsystem. From the data sequence output of the slow subsystem it is necessary to produce a data sequence with N times the sample rate in order to provide the data sequence input to the fast subsystem. Multi-rate data sequences can also be used to drive D to A (Digital to Analog) converters to reduce the dynamic errors and discontinuities associated with D to A outputs in a hardware-in-the loop simulation. This application of multi-rate data-sequence generation will be considered in Chapter 5.
Consider the dynamic system illustrated in Figure 4.4, where the slow subsystem is simulated with an integration step size equal to T and the fast subsystem is simulated with an integration step size equal to 
. Here N is an integer which represents the frame ratio of the multi-rate integration. Let 
be a data sequence from the slow subsystem with sample period T, where 
serves as an input to the fast subsystem. Assume that the fast subsystem integration algorithm requires inputs 
over the nth slow frame. The only way these fast data-rate sequence values can be calculated from the slow data-rate sequence data points, 
is through extrapolation. If 
and 
are state variables, then 
, are also available for the extrapolation formulas. If 
is a state variable and 
is integrated during
the nth frame to obtain 
before the N integration steps of the fast subsystem are mechanized, then 
is available as well as 
. In this case interpolation can be used to compute 
. Figure 4.5 shows three examples of the generation of a fast data sequence 
from a slow data sequence 
with N = 5. This means that the data rate of the fast data sequence is 5 times the data rate of the slow data sequence. In Figure 4.5a the fast data sequence is obtained by extrapolation based on 
and 
. In Figure 4.5b the extrapolation is based on 
and 
and is more accurate. In Figure 4.5c the fast data sequence is obtained by interpolation based on 
and 
. Clearly the interpolation algorithm provides a more accurate representation of the fast data sequence than either of the extrapolation algorithms shown in Figure 4.5.
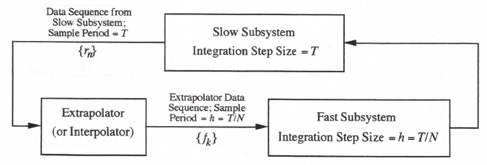
Figure 4.4. Multi-rate integration with extrapolator (or interpolator) to generate the multi-rate input to the fast subsystem from the slow subsystem output.
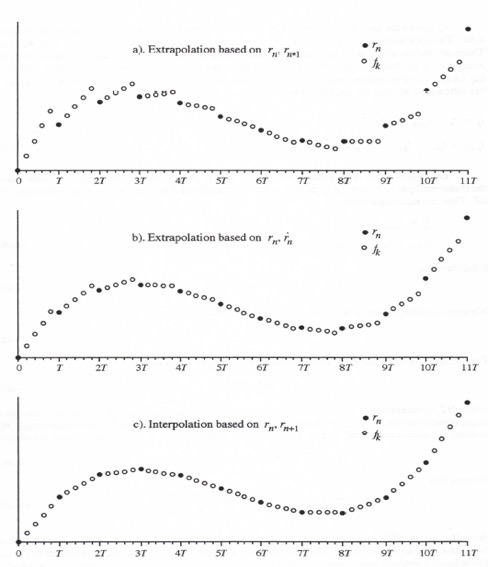
Figure 4.5. Generation of fast data sequence from slow data sequence, N = 5.
Consider the specific case where N = 5 and we use first-order extrapolation, as in Figure 4.5a. Then we need to compute estimates for 
and 
using 
, and 
. These estimates, along with 
, constitute the 5 data points in the 
data sequence over the interval 
, where the sample period of the fast data sequence is given by 
. In Eq. (4.2) for extrapolation based on 
and 
we set a = 0, 1/5, 2/5, 3/5 and 4/5, which leads to the following formulas for the fast data sequence: 
(4.39)
Let us now write the formulas for the fast data sequence points for the general case where the frame multiple is N and 
designates the extrapolated data point with extrapolation interval aT. Then the equations become
(4.40)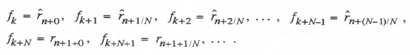 
It follows that
(4.41) 
We next consider a sinusoidal input data sequence. Thus we let
(4.42) 
The extrapolator response 
to the sinusoidal input 
is given simply by
(4.43) 
where 
represents the extrapolator transfer function for sinusoidal inputs for the dimensionless extrapolation interval a. Here we have designated the transfer function 
rather than simply 
in order to indicate its dependence on the interval a. Substituting Eq. (4.43) into (4.41), we obtain
(4.44) 
We note that
(4.45) 
Here 
and represents the ideal transfer function for the extrapolation interval a, first introduced as 
in Eq. (4.9). but now designated as 
to indicate its dependence on the dimensionless extrapolation interval a. Replacing T by Nh, n by k/N , and a by m/N in Eq. (4.45), we see that 
. When Eq. (4.45) is then substituted into Eq. (4.44), we obtain
(4.46) 
For all integer values k > 0 we rewrite Eq. (4.46) as
(4.47) 
Where
(4.48) 
It is clear that 
in Eq. (4.47) is simply a sinusoidal data sequence with sample period h, the integration step size for the fast subsystem. 
is equal to the ratio of 
, the extrapolator transfer function, to 
the ideal extrapolator transfer function; for both transfer functions the dimensionless extrapolation interval is m/N. We have already derived formulas for this transfer-function ratio in Sections 4.2 through 4.7 for a number of different extrapolation algorithms. From Eq. (4.48) we see that 
represents a periodic data sequence with period Nh, i.e., 
. This means that we can represent 
by means of a discrete Fourier series.* Thus we let
(4.49) 
Here 
is given by the sum of N sinusoidal data sequences of frequency 
, where 
, i.e., the frequency in radians per second of the fundamental component of the Fourier series.
To obtain the Fourier coefficients Cq we multiply both sides of Eq. (4.49) by 
and sum from k =0 to 
. Then
(4.50) 
Interchanging the order of summation on the right side of Eq. (4.50), we obtain
(4.51) 
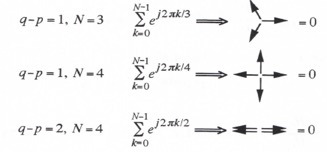
The exponential function 
is a complex number which can be represented as a unit vector in the complex plane. The polar angle of the unit vector is equal to 
, where both p and q are integers ranging between 0 and N-1. As k is indexed from 0 to N-1, it is easy to show that the sum of the unit vectors will add to zero except when p = q, in which case the sum is N. Shown below are several specific cases for illustrative purposes.
* Oppenheim, A.V., and R.V. Schafer, Digital Signal Processing, Prentiss-Hall, Englewood Cliffs, New Jersey, 1975.
It therefore follows that
(4.52)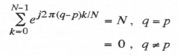 
Thus the double summation on the right side of Eq. (4.51) reduces simply to CqN and the formula for the Fourier coefficients becomes
(4.53) 
In particular 
, the discrete Fourier series coefficient for the zero frequency component of 
, is given by
(4.54) 
Thus 
is simply the average of the N extrapolator transfer function ratios 
corresponding, respectively, to the N extrapolation intervals 
Substituting the discrete Fourier series representation for 
, as given in Eq. (4.49), into Eq. (4.47), we have
(4.55)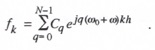 
This is the representation of the kth data point in the extrapolator output multi-rate data sequence with sample period h. The extrapolator input is the sinusoidal data sequence of Eq. (4.42) with sample period T (= Nh). The right side of Eq. (4.55) consists of N sinusoidal data sequences of frequency 
where 
, the slow data-sequence sample frequency. When we let the input frequency take on negative as well as positive values, as required in the exponential representation of sinusoids, then the frequencies contained in 
become 
. However, the amplitude Cq of the component with frequency 
, where 
, is normally small compared with the amplitude 
of the component at the original input frequency 
. To show this we let
(4.56) 
where 
and 
represent, respectively, the real and imaginary parts of the extrapolator transfer function ratio 
. For 
and 
, we have shown in Eqs. (1.52) and (1.53) that 
is approximately equal to the fractional error in gain of the transfer function and 
is approximately equal to the phase error of the transfer function. In Sections 4.2 through 4.7 we have derived exact and approximate formulas for 
and 
for a number of extrapolation algorithms, as summarized in Tables 4.1 and 4.2. In accordance with Eq. (4.48) k merely designates the appropriate dimensionless extrapolation interval a. Thus
Substituting Eq. (4.56) into Eq. (4.53), we obtain the following formula for the coefficient Cq in the discrete Fourier series representation of 
:
(4.57) 
From Eq. (4.52) we see that this can be rewritten as
(4.58)
and
(4.59) 
Thus the amplitudes Cq of the harmonic frequencies 
which are present in the extrapolated fast data sequence are indeed small for small 
and 
. The coefficient C0 in Eq. (4.59) simply represents the effective extrapolator transfer function for the slow input data sequence of frequency 
. It follows that
(4.60) 
and
(4.61) 
Here we have replaced 
and 
with 
and 
, respectively, where a = k/N. As a specific example, consider the case of first-order extrapolation based on 
and 
. Letting a = k/N in Eq. (4.11), we obtain the following formulas for 
and 
from Eqs. (4.60) and (4.61):
(4.62)
The same procedure is followed to obtain 
and 
, the multi-rate extrapolator gain and phase errors, respectively, for other extrapolation algorithms. The actual errors depend on the frame-rate multiple N. For 
the summations in Eqs. (4.60) and (4.61) are replaced by the following integrals:
(4.63)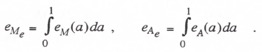 
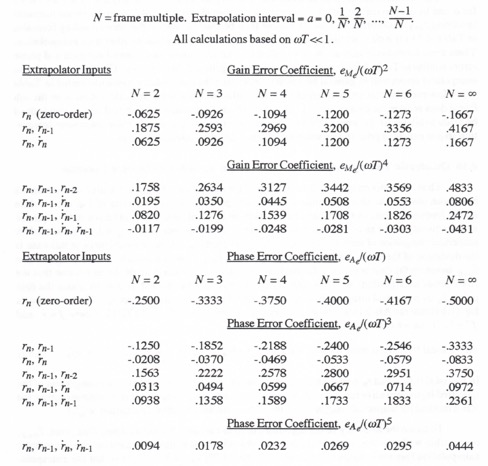
Table 4.3 summarizes the multi-rate extrapolator gain and phase errors for all of the extrapolator algorithms considered in this chapter. The table shows numerical values for the error coefficients when the frame multiple N = 2, 3, 4, 5, 6 and 
. Note that the case of zero-order extrapolation is also included in the table. This is in effect equivalent to no extrapolation at all; i.e., the fast frame-rate system simply uses the same input 
from the slow system for each of the N fast-system frames until 
, the next input from the slow system is available. In this case the extrapolation algorithm is given by
(4.64) 
and the extrapolator transfer function 
. After division by the ideal extrapolator transfer function, 
and subtraction of 1, we obtain the following formulas for the exact and approximate fractional error in the zero-order extrapolator transfer function:
(4.65) 
It follows that the fractional error in gain and the phase error for the zero-order extrapolator are given , respectively, by
(4.66) 
These formulas are then used in Eqs. (4.60) and (4.61) with a=k/N to compute the fractional gain error, 
, and the phase error, 
, when zero-order extrapolation is used to generate the multi-rate data sequence.
Next we consider the dynamic errors in generating the multi-rate data sequences using interpolation instead of extrapolation. We note that the formulas for interpolation can be obtained from the formulas for extrapolation by simply replacing a with a– 1 and n with n + 1. For example, when these substitutions are made in Eq. (4.2), the following formula is obtained for interpolation over the nth frame based on 
and 
:
(4.67) 
Also, the asymptotic formulas for the gain and phase errors for interpolation based on 
and 
Table 4.3
Summary of Multi-rate Extrapolator Gain and Phase Errors
are generated by replacing a with a-1 in Eq. (4.11) for 
and 
. In this way we obtain
(4.68) 
where in this case T rather than h is designated as the step size. Note that 
and 
now vanish in Eq. (4.68) at a= 1 as well as a = 0. Also, the gain-error coefficient in Figure 4.1 over the interval 
for extrapolation based on 
and 
becomes the gain-error coefficient over the interval
for interpolation based on 
and 
. It is then apparent that interpolator errors over the interval 
are much smaller than extrapolator errors over the same interval.
The substitutions used to generate Eq. (4.67) from Eq. (4.11), namely n + 1 for n and a— 1 for a, can be used to convert all of the extrapolation formulas in Table 4.1 to interpolation formulas involving 
. Substitution of a-1 for a can then be used to convert the corresponding formulas in Table 4.2 to transfer-function gain and phase errors for interpolation rather than extrapolation. These error formulas in turn allow us to calculate a table of multi-rate interpolator gain and phase errors similar to Table 4.3 for multi-rate extrapolator gain and phase errors. Clearly the multi-rate interpolator errors will in general be much smaller than the extrapolator errors illustrated in Table 4.3. However, utilization of interpolation for multi-rate data-sequence calculation over the nth frame does require the data point 
. In the multi-rate simulation of Figure 4.4, 
can indeed be made available for generating the fast data sequence points 
if the nth slow-subsystem integration step is executed prior to executing the N fast-subsystem integration steps.
4.10 Quadratic Extrapolation Errors based on an AB-2 Reference Solution
Thus far in this chapter all the extrapolator (or interpolator) formulas for time-domain errors have been based on an ideal reference data sequence given by the Taylor series of Eq. (4.3), while all the frequency-domain errors have been based on an ideal sinusoidal reference data sequence with frequency 
. In an actual simulation, however, data sequence points 
will be generated by numerical integration of state-variable derivative data points 
. Of more significance in this case is the deviation of the extrapolated data-sequence value 
from a reference data-sequence value 
based on the data points 
. To illustrate how this calculation is made, let us assume that the AB-2 predictor algorithm, which is often the preferred real-time method, is used to obtain the data points 
by numerical integration of the state-variable derivative data points 
. We have seen in Eq. (1.14) that the AB-2 local integration truncation error is equal to 
, where 
and 
. Thus we can write 
(4.69)
In Eq. (4.69) 
and 
represent the data-sequence values resulting from exact integration of the specified input derivative function f(t), whereas 
and 
represent data points obtained using the AB-2 method for numerical integration of the state-variable derivative data sequence 
.
To make the accuracy of the algorithm used to calculate the extrapolated data point, 
, compatible with the step-by-step accuracy of the AB-2 integration, we assume that a quadratic extrapolation formula is utilized. Thus Eqs. (4.26), (4.29) and 4.34) all show that the extrapolation error when using quadratic methods is proportional to 
i.e., 
: the same as in Eq. (4.69) for the local integration truncation error when using the second-order AB-2 method. The following formula represents a numerical approximation to 
, i.e., 
, based on the exact data sequence values 
and 
:
(4.70) 
The right side of Eq. (4.70) represents a backward difference approximation for 
, where it is easy to show from Taylor series expansions for 
and 
about 
that the error in the
approximation is proportional to 
, i.e., 
; It is useful to note that the numerator of the right side of Eq.(4.70) can be rewritten in terms of the AB-2 data points 
and 
in the following way:
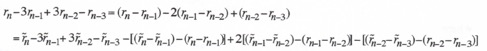or 
(4.71)
To examine the dependence of both truncation errors and quadratic extrapolation errors on 
, we next let 
, which means that 
constant. Eq. (4.71) that the local truncation error will then be independent of the index n, which means that the local-truncation error terms on the right side of Eq. (4.71) will cancel each other. Thus we can write
(4.72) 
It follows that whether quadratic extrapolation uses the exact data points 
or the data points 
obtained by AB-2 integration, the third time derivative of r will be the same constant and hence the approximate quadratic extrapolation errors will be the same. This in turn means that the extrapolation error formula in Eq. (4.26), which assumed quadratic extrapolation based on 
and 
, will apply equally well when the quadratic extrapolation is based on data points 
, as generated by AB-2 integration.
Next we consider quadratic interpolation based on 
and 
. As noted at the end of Section 4.9, 
can be made available in the nth integration frame for the multi-rate interpolation of Figure 4.4 if the slow subsystem integration step is executed prior to executing the N fast-subsystem integration steps. When using predictor integration methods such as AB-2, 
can always be made available at the start of the nth frame if both r and 
are state variables, since in this case 
is available at the end of the n – 1 frame to implement the AB formula for 
. As noted earlier, we can obtain the formula for quadratic interpolation based on 
, 
and 
by replacing a with a-1 and n with n + 1 in Eq. (4.21). In this way we obtain
(4.73) 
Substituting a -1 for a in Eq. (4.26), we obtain the following formula for the approximate time-domain error:
(4.74) 
Again substituting a-1 for a in Eq. (4.24), we obtain the following formulas for the fractional gain error and phase error for quadratic interpolation based on 
, 
and 
:
(4.75) 
Note that the time-domain and frequency domain errors in Eqs. (4.74) and (4.75) now vanish for a = 1, 0 and -1, corresponding to 
and 
, respectively.
An alternative to Eq. (4.73) for implementing quadratic interpolation based on 
, 
and 
is to use the first three terms of the Taylor series of Eq. (4.3). Thus we have
(4.76) 
where
(4.77) 
Here the formulas in Eq. (4.77) represent central-difference approximations for the first and second time derivatives, respectively. In each case Taylor series expansions for 
and 
can be used to show that the errors in the approximations are proportional to 
. When the formulas in Eq. (4.77) are substituted into Eq. (4.76), Eq. (4.73) is obtained. The following formula represents a numerical approximation to 
, i.e., 
, based on the exact data sequence values based on the exact data sequence values 
and 
:
(4.78) 
Following the same procedure used to derive Eq. (4.72), we can show that
(4.79) 
It follows that whether quadratic interpolation uses the exact data points 
or the data points 
obtained by AB-2 integration, the third time derivative of r will be the same constant and hence the approximate quadratic interpolation errors will be the same. This in turn means that the error formulas in Eqs. (4.74) and (4.75), which assumed quadratic interpolation based on 
will apply equally well when the quadratic interpolation is based on data points 
as generated by AB-2 integration.
In Figure 4.6 the quadratic extrapolation/interpolation errors given by Eqs. (4.26) and (4.74), made dimensionless through division by 
, are shown as a function of the dimensionless extrapolation interval a. We recall that the extrapolation for generating the fast data sequence 
from the slow data sequence 
, as utilized to obtain the input to the fast subsystem in the multi-rate integration shown in Figure 4.4, requires a dimensionless extrapolation interval a that ranges from 0 to 1. Over this interval, 
, Figure 4.6 shows the much better accuracy of extrapolation based on 
and 
(heretofore called interpolation) compared with extrapolation based on 
and 
.
At this point it is useful to note that an estimate 
for 
can be calculated with quadratic extrapolation based on 
and 
by using Eq. (4.21) with a = 1. Thus when we let a = 1 in Eq. (4.21), we obtain
(4.80) 
When 
is substituted for 
in Eqs. (4.76) and (4.77), the result is a quadratic extrapolation formula for 
that is the exact equivalent of the earlier formula in Eq. (4.21). From Eq. (4.26) we see that the error in 
when calculated using Eq. (4.80) is equal to 
, at least to order 
. If we then add 
from Eq. (4.78) to the right side of Eq. (4.80), the error of order 
in 
will be cancelled. In this way we obtain the cubic extrapolation formula
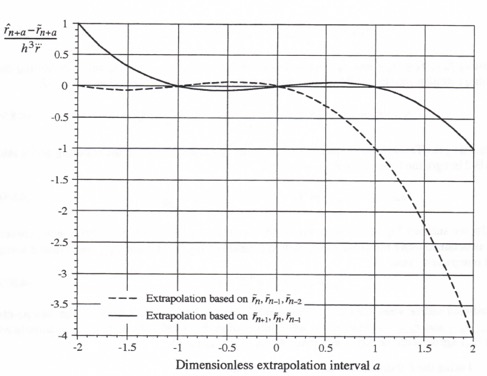
Figure 4.6. Errors for quadratic extrapolation based on 
and 
.
which now represents an approximation to 
which is accurate to order 
. It follows that if we substitute 
from Eq. (4.81) for 
in Eqs. (4.76) and (4.77), the resulting quadratic extrapolation for 
will to order 
yield the same accuracy as that given by Eq. (4.74). Thus when 
is not available for extrapolation over the nth frame, we can still achieve the equivalent accuracy, at least approximately, by utilizing Eq. (4.81) to estimate 
.
Consider next the case where the cubic extrapolation formula of Eq. (4.81) is based on data points 
and 
as obtained by AB-2 integration of the data sequence 
. Then we can rewrite Eq. (4.81) in the following way:
(4.82) 
From the AB-2 integration formula we note that 
(4.83)
In terms of the state-variable derivative data points 
, Eq. (4.82) can then be rewritten as
(4.84) 
Rewriting 
and 
using Taylor series expansions about fn and substituting the resulting formulas into Eq. (4.84), we obtain the following series representation of 
:
(4.85) 
Again, using the Taylor series expansion about 
for 
and substituting the resulting series into the AB-2 integration formula for 
, we obtain
(4.86) 
Finally, we subtract Eq. (4.86) from Eq. (4.85) to obtain the formula for the difference between 
, as obtained using the cubic extrapolation formula of Eq. (4.81), and 
, as obtained using AB-2 integration. Thus
(4.87) 
As predicted earlier, when the cubic extrapolation formula of Eq. (4.81) is based on the data points 
and 
as obtained by AB-2 integration, Eq. (4.87) shows that the extrapolated result 
agrees with the AB-2 integration result 
to order 
Taking the Z transform of Eq. (4.87), we obtain
(4.88) 
For a sinusoidal data sequence with 
, it follows that 
and 
. Also, to order 
. Thus 
and 
. Letting 
, we can then rewrite Eq. (4.88) as
or
(4.89) 
Substituting the approximation 
for 
and dropping terms of order 
and higher on the right side of Eq. (4.89), we obtain
(4.90) 
Here the left side of Eq. (4.90) represents the fractional error in the transfer function relating 
as obtained from the data points 
and 
using the cubic extrapolation formula of Eq. (4.81), to 
as obtained by AB-2 integration of the data sequence 
. Again, we recall from Eqs. (1.53) and (1.54) that the real and imaginary parts of the fractional error in any transfer function represent, respectively, the fractional error in transfer-function gain and the transfer-function phase error. Therefore, from the right side of Eq. (4.90) we conclude that for sinusoidal inputs f of frequency 
, the extrapolated result 
matches the AB-2 result 
except for a fractional gain error of approximately 
, with zero phase error to order 
. Clearly 
matches 
exactly to order 
, which is what we concluded earlier in deriving Eq. (4.81).
4.11 Summary of Extrapolation Methods
In this chapter we have derived extrapolation formulas for estimating future values of a time-dependent function based on current and past values of a data sequence representing the function. We have also presented formulas for the approximate time-domain error for each extrapolation method as a function of the dimensionless extrapolation interval a. Table 4.1 summarizes the formulas for linear, quadratic and cubic extrapolation. Formulas for the approximate gain and phase shift of the extrapolator transfer function for sinusoidal inputs are given in Table 4.2 for each extrapolation method. The higher-order extrapolation formulas, e.g., quadratic and cubic methods, produce more accurate results but require more calculations. They also respond less favorably to any discontinuities represented by the data sequence.
Because the generation of fast data sequences from slow data sequences, as required in multi-rate integration, constitutes one of the principle applications for digital extrapolation, we derived formulas in Section 4.9 for multi-rate extrapolator gain and phase errors for the different extrapolation methods. Again, the higher order methods are in general more accurate but require more calculations. It should also be noted that the higher order methods, when used for slow-to-fast subsystem interfacing in multi-rate integration, can lead to numerical instabilities for large integration step sizes when the slow and fast subsystems are tightly coupled in a closed loop. In particular, the cubic extrapolation represented by Eq. (4.81), while almost exactly matching the output of second-order integration one step in the future, should be used with care in multi-rate simulation of tightly-coupled systems.
